[最新] Xとyを使った式 225514-Xとyを使った式

文章問題の考え方講座 Part3 1 次世代型個別指導塾アチーブメント Achievement
未知数と変数 数量の関係を考えるとき,大きさがわかっていない数量を やxなどを使って表しますが,その やxを未知数といいます。 これに対して,大きさがきまっていない数量を やxなどを使って表したとき,それらを変数といいます。 未知数といった別エントリで楕円の当てはめのスクリプトを書いているのですが,どうも楕円のプロットのさせ方がいまいちピンと来なかったのでまとめます.ここで最終的に解決しようとしている問題は 楕円の方程式として f(x, y) = 0 が与えられたときに,どうやって Python を使ってプロットする
Xとyを使った式
Xとyを使った式-求められた複素数をxy直交座標で表せば、$(x\cos\theta y\sin\theta, x\sin\theta y\cos\theta)$となって、やはりはじめに示した式と同じになります。 座標回転の式を使った作例 座標回転の式を使った作例もひとつご紹介しておきましょう。1 鉛筆1本の値段をX円,10本の代金をY円として,XとYの関係について 考えましょう。 ⑴ XとYの関係を式に表しましょう。 式 ⑵ Xに50をあてはめて,代金を求めましょう。 ⑶ Xの値を60にしたとき,それに対応するYの値を求めましょう。

世界一分かりやすい算数 小6 文字と式
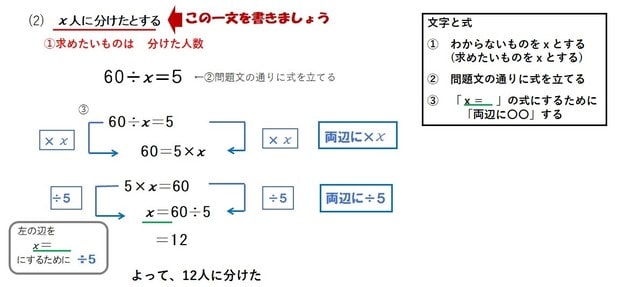
中学1年で「正の数・負の数」の次に学習するのが、「文字の式」です。 「文字の式」の単元では、a、b、c、 x 、 y などのアルファベット、つまり文字と数を使った式の計算を学習します。 はじめて文字の式を学習した中学生の多くは、次のような疑問を持つことと思います。2 文字を使った式 ・未知数をxとして、問題場面を立式し、問題の解決に用いる。 ・未知数をxとして問題場面を立式し、xの値の求め方を考える。 ・1量だけの数値がわかっている問題場面において、変数をxとして、問題場面を式に表すことができる。= という式になればOKです。 ここで登場する と は変数としての記号なので、6年生で登場するxとyと同じ役割です。 (我々の時代は中学数学で登場でしたが) 一見すると と を使って式にあらわすのは、簡単そうに感じますよね。 しかし、第一の
方程式の計算問題の説明は以上です。 数学はスポーツと同じで、例を見たあとに自分で問題を解いて計算方法を身につけていくものです。 問題に応じて等式の性質が反射的に出てくるまで、解いて解いて解きまくりましょう! なお、一次方程式の解き方これで、xとpの一般解が求められました。 次に、これをxとyの一般解に直します。 3)式(A)と式(D)を連立してxとyだけの式にする。 式(D)を変形して、 (3xp2p^2)p=c ⇔{2(2xpp^2)xp}p=c ←式(A)の右辺にあわせて変形。 これと式(A)を連立して、文字と式 小6 基本は を使った式と同じです 算数の教え方教えますmother S Math Happy Study Support 小学校6年生 算数 文字を使った式 Xを求めよう たし算 Youtube 6年生算数ドリル 文字と
Xとyを使った式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Yfetwcxhshmyom |  Yfetwcxhshmyom | Yfetwcxhshmyom |
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom | Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom | Yfetwcxhshmyom | Yfetwcxhshmyom |
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom | Yfetwcxhshmyom | Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom | Yfetwcxhshmyom | Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom | Yfetwcxhshmyom |
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom | Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom | Yfetwcxhshmyom |
 Yfetwcxhshmyom | Yfetwcxhshmyom | Yfetwcxhshmyom |
Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
「Xとyを使った式」の画像ギャラリー、詳細は各画像をクリックしてください。
 Yfetwcxhshmyom |  Yfetwcxhshmyom |  Yfetwcxhshmyom |
 Yfetwcxhshmyom | 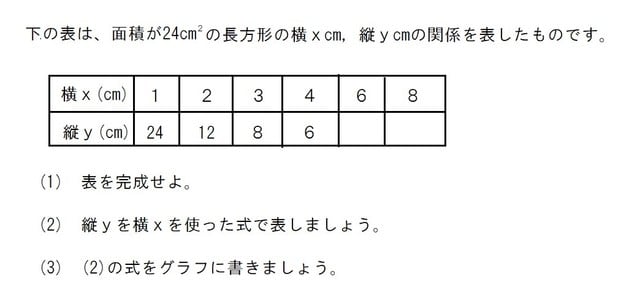 Yfetwcxhshmyom |
文字を使った式のドリル 文字を使った関係式を表す練習をします.たとえば,えんぴつ1本の値段を x 円として12本買った場合の代金を y 円として式をたてます. 例) x ×12= y x などの文字を使った代数式のドリルを作成します.例に示しているようにまずは、変数のおきかえをする方法です。 この方法が一番実践的な方法だと思います。 本質的にはユークリッドの互除法と同じ方針ですが、 変数の置きかえをすることで、式変形の見通しがよくなるのがメリットです。 \(x,\;
Incoming Term: xとyを使った式,
コメント
コメントを投稿